This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
Authors:
(1) H. Wen, Department of Economics, University of Bath;
(2) T. Huang, Faculty of Business and Law, University of Roehampton;
(3) D. Xiao, School of Mathematical Sciences.
Table of Links
Relevant Blockchain Technologies
Advanced Models for Real-World Scenarios
Future Investigations, and References
5. Monte Carlo Simulations
Having meticulously constructed our models in preceding sections, it’s now imperative to subject them to rigorous simulations and discern whether their performance aligns with our expectations. Central to our simulation methodology is the renowned Monte Carlo technique. We begin our journey with a Brief Introduction to Monte Carlo Simulation, setting the stage for newcomers and grounding our approaches in a theoretical foundation. We then delve into the General Settings for Monte Carlo Simulation of the Reputation System, laying out the parameters and configurations vital for our experiments. Two contrasting initial credit distribution scenarios are subsequently examined: one where Scenario of Credit Points Uniformly-Distributed among Agents Initially, and another highlighting a Scenario of Credit Points Initially Distributed in Power-Law among Agents. As we venture deeper into the simulation results, our focus bifurcates into two segments: the Results and Interpretations of Monte Carlo Simulations for the Basic Model and the Results and Interpretations of Monte Carlo Simulations for Advanced Models, each shedding light on their respective model outcomes and drawing comparisons where necessary.
5.1. Brief Introduction to Monte Carlo Simulation
Monte Carlo Simulation (MCS) [80] is a powerful statistical technique that enables a probabilistic approach to comprehending complex systems. Essentially, MCS employs random sampling and statistical analysis to approximate solutions to mathematical challenges.
5.1.1. Basic Principles
The central concept of MCS is simple: by executing a large enough number of random simulations or ”trials”, one can derive an approximation of a desired quantity. Mathematically, let’s take a random variable X with an expected value E[X]. The Monte Carlo estimate of E[X] is:
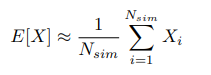

5.1.2. Application to Structural Reliability
In structural engineering, from which MCS has its origins [81], MCS has become an essential tool for gauging the reliability of structures. Let’s consider a limit state function (LSF) G(x) that delineates the boundary between failure and successful states of a structure. A typical representation is:
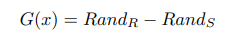
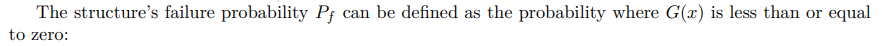
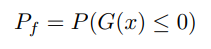
To estimate this failure probability through MCS, one can:

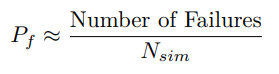

5.1.3. Limitations and Considerations

5.2. General Settings for Monte Carlo Simulation of the Reputation System
Within complex reputation systems, particularly those governed by mechanisms like ’staked credit points’, the challenge lies not just in constructing a robust theoretical framework, but also in validating its viability in diverse real-world scenarios. Here, the Monte Carlo simulation stands as a quintessential tool, bridging the often-gaping chasm between theoretical robustness and empirical efficacy. By simulating numerous rounds of agent actions, rating, and adjustments, we can gain insights into the system’s stability, the distribution of credit points, and the effectiveness of the staking mechanism in promoting desired actions.
The nature of staking, especially with non-traditional metrics like ’credit points’, introduces layers of variability and potential strategic actions by participants. The Monte Carlo simulation, with its inherent stochastic modeling, enables a comprehensive exploration of these actions under myriad conditions. By running numerous simulations, each representing a possible state of the world, it unveils vulnerabilities, strengths, and unforeseen outcomes tied to the system.
This systematic exploration also establishes a rating loop. Findings from the simulation can guide refinements in the underlying model, ensuring that the reputation system remains adaptive and resilient. For instance, should simulation results indicate certain strategies where producers might overly centralize staking, the theoretical constructs can be adjusted to deter such actions, thereby ensuring a more equitable and effective system, if it is what the model aims for.
To underscore its significance: the Monte Carlo method isn’t merely a testing instrument. It’s an iterative dialogue between the abstracted world of theory and the unpredictable terrains of practical application. In the context of a reputation system driven by ’staked credit points’, this dialogue is crucial, fortifying the model’s architecture against real-world exigencies and guaranteeing its longevity and relevance.
The results of the MCSs will be illustrated and discussed in detail in Section 5.5 and Section 5.6. It’s worth noting that some anomalies were observed within the results of our MCSs. These outlier data points can be attributed to the inherent randomness and stochastic nature of the simulation method. Monte Carlo, by its design, employs random sampling to obtain numerical results for problems that might be deterministic in principle. While the law of large numbers ensures that these simulations converge to the expected value over a vast number of runs, occasional deviations from the expected outcome are not only possible but expected due to this randomness. Detailed examination of these anomalies provides insights into the range of possible outcomes, even if they occur with low probability.
5.2.1. Division of Staking Rates Between Actions and Ratings

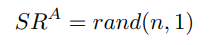

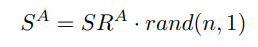
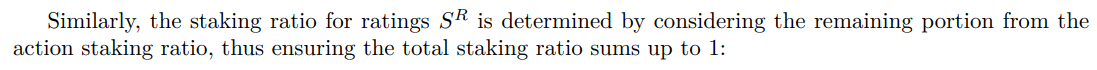

5.3. Scenario of Credit Points Uniformly-Distributed among Agents Initially
In the context of our reputation system theoretical model, we employ Monte Carlo simulation to generate synthetic data that adheres to specific statistical properties. For the initial MCS of the reputation system model, we propose an approach where each agent is initially provided with an equal share of credit points. Agents, with their respective credit point allocations, will then randomly determine a staking ratio for various activities within the system. The core intention behind this setup is to examine if such an even distribution combined with a random staking approach can incentivize active participation and promote positive actions among agents.
Every agent Ai in the system, where i ranges from 1 to n (total number of agents), starts with an equal amount of credit points:

where CPtotal is the total amount of credit points in the system.


With uniform initial credit point distribution and random staking ratios, the system’s primary goal is to understand if agents are inclined towards positive participation. Key points of examination include:
• Active Participation: Whether agents, having an equal footing at the beginning, are more likely to participate actively.
• Risk and Reward Analysis: How agents balance their staking decisions when the potential rewards and risks are uncertain.
• Action Dynamics: If and how agents adjust their staking ratios based on observed outcomes, either from their own actions or from the actions of other agents.
This model offers a fresh perspective on agent action when introduced to a reputation system that starts with equality and then introduces randomness in staking decisions. By monitoring the agents’ actions under these conditions, we can gain insights into the optimal strategies and adjustments required to foster a more cooperative and engaged environment.
5.4. Scenario of Credit Points Initially Distributed in Power-Law among Agents
One of the fundamental challenges in designing any computational model is selecting the right initial conditions and distributions that mirror the complexity and irregularity of the real world. Empirical studies across numerous domains, ranging from economics to natural phenomena, often demonstrate that certain systems do not follow a simple uniform distribution. Instead, they lean towards distributions characterized by a power law.
The Pareto Principle, colloquially known as the 80-20 rule, is a striking manifestation of power law distributions in socio-economic settings. It suggests that roughly 80% of the effects come from 20% of the causes, be it wealth distribution, sales figures, or other phenomena. Rooted in both economic reasoning and mathematical underpinnings, this principle highlights the skewed nature of many real-world distributions.
In light of this, while beginning with a uniform distribution offers a clean, symmetric baseline for our model, it’s imperative to also examine the action under power law distributions. By doing so, we can ensure our model’s robustness and its capability to generalize to real-world scenarios where inequalities and imbalances are often the norm.
In the random sampling of MCS, one of the primary challenges is the generation of random numbers that adhere to a non-uniform distribution, such as the power-law distribution. The inverse transform method offers an elegant solution to this problem [82, 83, 84, 85, 86].
5.4.1. Inverse Transformation Method
The inverse transformation method is a fundamental technique for generating random samples from a specified distribution. By utilizing the inverse of the cumulative distribution function (CDF) — which is derived from the probability density function (PDF) for continuous variables and the probability mass function (PMF) for discrete variables — this method can transform uniformly distributed random numbers, typically from the interval (0, 1), into values consistent with the target distribution. Referring to the CDF formula 9 in Section 3.4, we categorize the application of this method into two scenarios: continuous and discrete.

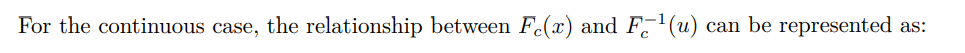

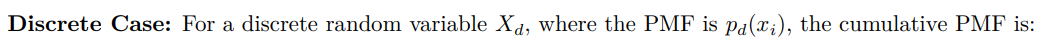
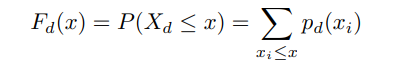

5.4.2. Application of the Inverse Transformation Method to Power-law Distributions
Power-law, also known as Pareto distributions, appear frequently in various natural and societal phenomena. They are characterized by ”heavy tails”, indicating that tail events (those of low probability) are still notably impactful.
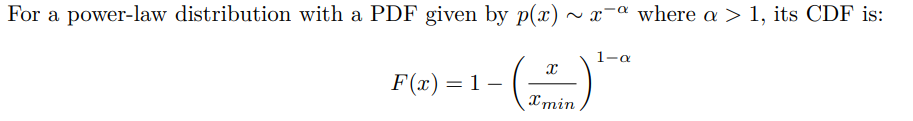
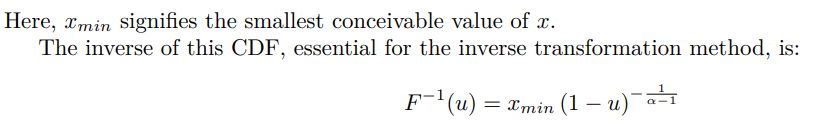
The inverse transformation method is favored when modeling systems with power-law traits due to:
• Its straightforward implementation, exemplified by the analytical form of the inverse CDF in equation (34).
• Its aptness at mirroring the unique heavy-tailed nature innate to power-law distributions.
However, for distributions lacking a defined inverse CDF, the method might be less efficacious. Such scenarios would require iterative numerical procedures, potentially augmenting computational costs and introducing potential inaccuracies.
In summation, the inverse transform method adeptly translates uniformly distributed random numbers to ones adhering to a non-uniform distribution. In our reputation system model, this methodology proved invaluable for generating synthetic data that mirrored a power-law distribution, affirming the model’s authenticity and precision.
5.5. Results and Interpretations of Monte Carlo Simulations for the Basic Model
Following the preparations outlined in Section 5.2, we seamlessly executed MCSs on the basic model. The outcomes aligned perfectly with our expectations generated from Section 3.
5.5.1. Credit Point Dynamics based on Agent Actions
In our model, the implications of agent actions are distinctly reflected through the benefits or penalties they accrue in the form of credit points. Our MCSs categorically delineate agents into two prominent categories based on the mean values assigned to their actions with a smaller variance than that across agents, as introduced in Formula 8 of Section 3.4.
1. Beneficial Actors: Agents endowed with higher mean action values in the simulations invariably experience positive returns when evaluated by their peers. The magnitude of their credit point gains is directly proportional to the amount they staked during their actions and the stake amount of the evaluating peers.
2. Detrimental Actors: Conversely, agents assigned lower mean action values incur losses in credit points when evaluated. Similar to the beneficial actors, the quantum of these losses is directly influenced by the agent’s staked amount during their actions and the stake of the evaluating counterparts.
To analyze the variation in action levels among agents, we use the variable CDF, as defined in Formula 9 of Section 3.4. As the simulation progresses, differences in credit point distributions become more pronounced based on agents’ action quality. This leads to a clear trend: agents with consistent positive actions experience an increase in benefits, while those with negative actions face mounting penalties.
5.5.2. Stake-to-Reward Relationship with respect to Ratings
Our MCSs, initiated with a uniform distribution of credit points, elucidate the intricate dynamics between agent actions and the progressive distribution of credit points. As the simulation progresses, we observe that the cumulative benefit or loss an agent incurs for each review is primarily determined by two pivotal factors: the sign (positive or negative) of their review for a particular agent, and its alignment or disparity with the majority consensus. Furthermore, the magnitude of these benefits or losses is also proportionally affected by the amount an agent pledges during the review, as well as the pledges made by other reviewers. Essentially, the staked amount acts as a multiplier, amplifying the potential gains or detriments. Therefore, agents will experience varying cumulative gains or detriments over time. These cumulative benefits, or the sum of individual rating outcomes, depend on factors like the magnitude of their own and other raters’ stakes, and especially, the degree of alignment of their ratings with the prevailing majority opinion.
In the context of a power law distribution, our conclusions remain strikingly similar. Our simulations, initialized with agents adhering to a power law distribution of credit points, underscore the complex relationship between individual agent actions and the ensuing distribution dynamics. It becomes evident that an agent’s cumulative gain or loss from each evaluation is fundamentally governed by the polarity (positive or negative) of their feedback for a given agent and its congruence or divergence from the majority consensus. The cumulative benefits, being an aggregate of outcomes from individual ratings, are influenced by various factors: an agent’s rating frequency, the quantum of stakes they commit during their evaluations, and predominantly, the extent to which their feedback mirrors the predominant majority viewpoint.
5.6. Results and Interpretations of Monte Carlo Simulations for Advanced Models
It is crucial to simulate more advanced models that closely resemble real-world scenarios. This step is imperative to understand the dynamics and implications of the proposed system comprehensively. Furthermore, before the formal launch of the reputation system, extensive real-world testing with actual users is of paramount importance to ensure the robustness and reliability of the system. This not only helps in identifying potential challenges but also aids in refining and optimizing the model for practical applications.
5.6.1. Adaptive Model with Learning and Adjustment
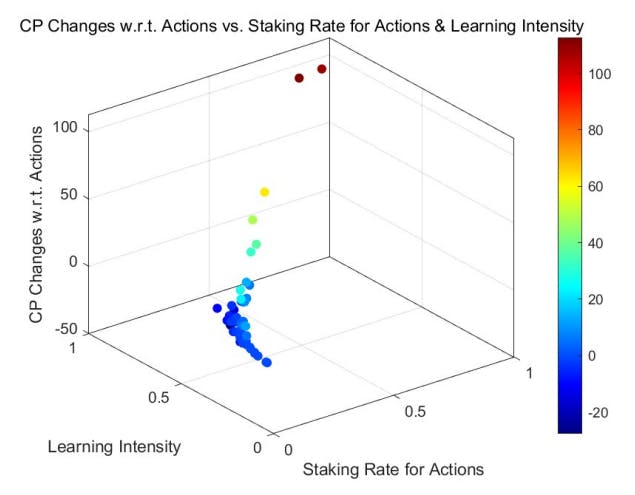
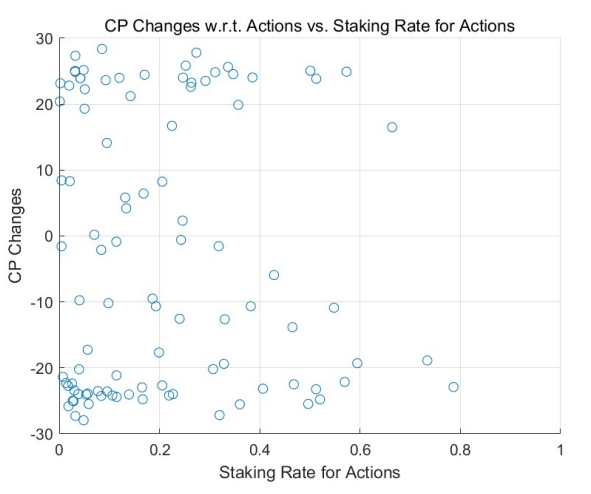
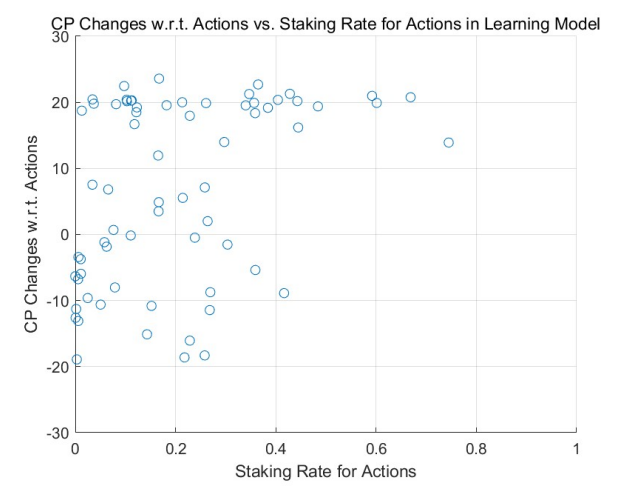
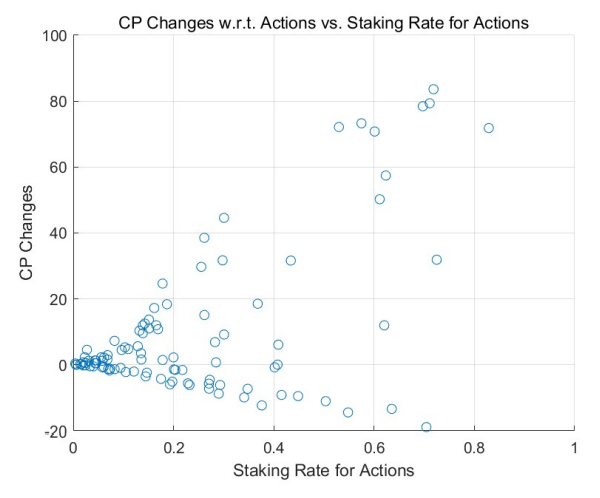
Based on the theoretical analysis in Section 4.2, we discern a marked difference between the adaptive model with learning and adjustment and the non-learning models regarding staking on actions. As rounds progress, agents with positive returns—often acknowledged by their peers—increase their staking, enhancing their rewards. Conversely, agents experiencing negative returns, mainly due to unfavorable ratings, decrease their staking, thereby reducing their losses. The magnitude of these adjustments correlates with learning intensities (denoted by αL, as discussed in Section 4.3) and the return outcomes until the staking rate approaches 0 or 1, at which point intervals become negligible.
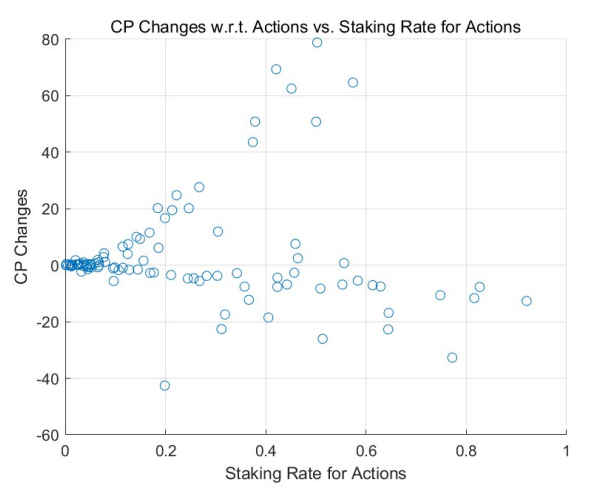
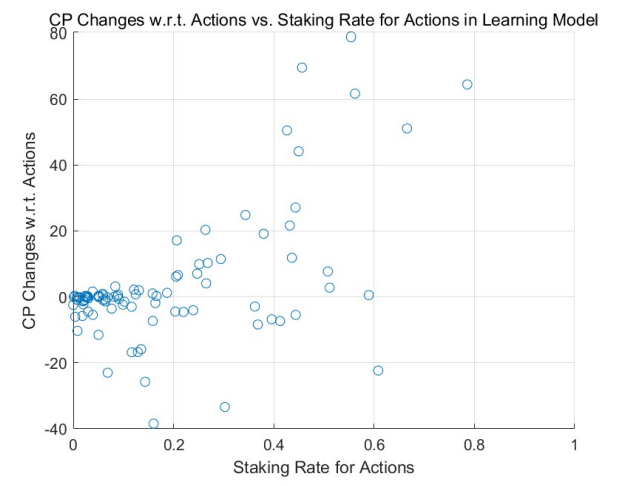
This behavior is corroborated by the results of Monte Carlo simulations (MCS), particularly in highstaking regions. A comparative study between the adaptive learning model (see Figure 3 for a uniform initial distribution and Figure 5 for a power-law initial distribution) and the non-learning model (refer to Figure 2 and Figure 4) underscores this trend. Agents with positive outcomes increase their staking in high-staking
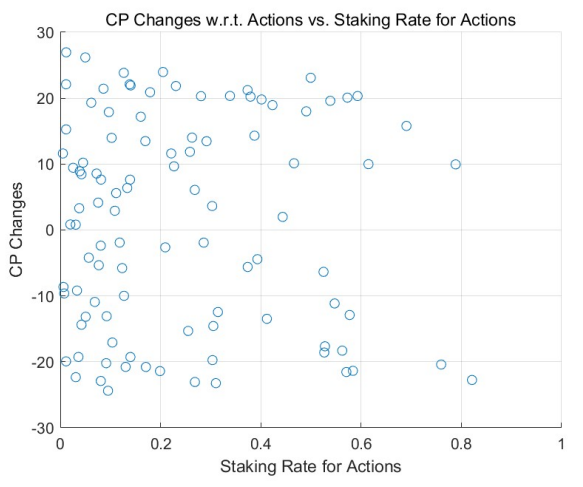
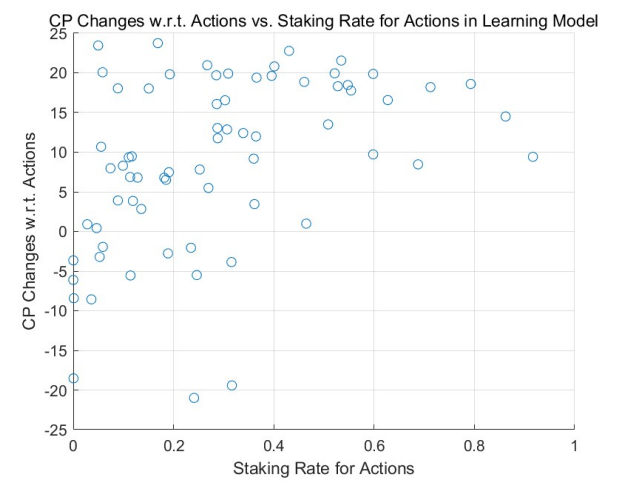
regions, as evident in the right portions of the figures. In contrast, those with negative results decrease their stakes, gravitating towards the left of the diagrams.
Over multiple rounds, the adaptive model with learning and adjustment demonstrates a rise in agents achieving positive returns in high-staking actions, while the non-learning model shows a decline in such agents. This dynamic resembles the natural evolution of free markets where specialists excel in their domain, echoing the adage, ”the most adept individuals handle the most nuanced tasks.”
Within the learning model, we utilized Monte Carlo simulations to assess varying learning intensities (denoted by αL) among agents, elaborated further in Section 4.3. We explored two scenarios: uniform learning intensity across agents and individual intensities.

We pursued two approaches for individualized learning intensities. Initially, we assigned random values
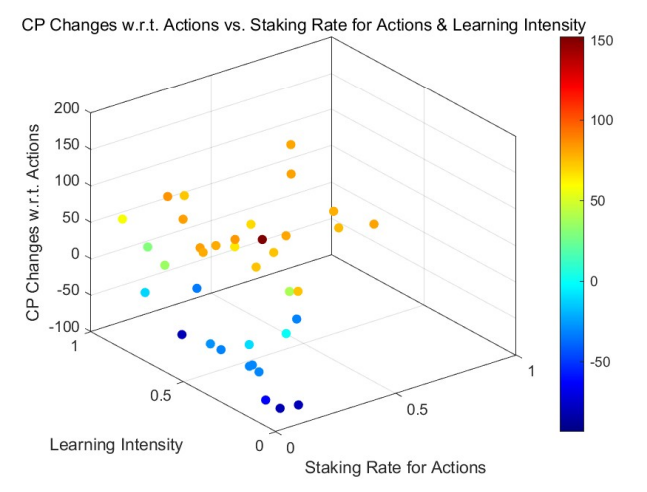


For both approaches, the overarching trends are consistent: Agents with higher learning intensities tend to experience amplified credit gains and fewer losses. Influenced by previous outcomes, they adjust their stakes, optimizing their risk-reward balance.
Notably, the patterns are more pronounced in Figure 8 and Figure 9 than in Figure 6 and Figure 7. This distinction arises from the cumulative effect of increasing both staking and learning intensities over rounds, suggesting that credit changes align with these intensities over time.
Moreover, the differences between Uniformly-distributed and Power-Law-distributed initial credit points are consistent with our prior discussions. The role of learning intensity in altering credit points remains
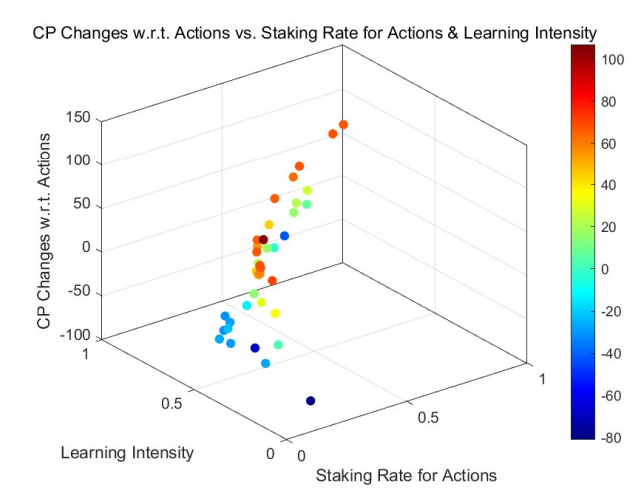
uniform across varying initial distributions, with the Power-Law distribution maintaining its long-tail effect.
In contrast to staking on actions, the discrepancy between the adaptive and non-learning models concerning staking on ratings is more subtle. This nuance originates from the complexities of learning from rating consequences. Agents benefit when their ratings align with the majority but face challenges when they differ. This variance somewhat moderates the ”Keynesian Beauty Contest” effect [87], where agents anticipate majority ratings rather than providing genuine assessments.
These simulation results resonate with the theoretical insights from Section 4.3. They suggest our blockchain-centric reputation system effectively establishes an on-chain market mechanism, adeptly avoiding the challenges of falsified ratings prevalent in traditional third-party vendor platforms, as highlighted in Section 1.
5.6.2. Allowing Agents to Skip Rounds
We have developed a MCS program that incorporates the mechanism allowing agents to skip rounds. Specifically, in each round, a certain proportion of agents will neither perform any actions nor provide any ratings. Unless otherwise specified, all subsequent simulation results presented will account for this skipping mechanism.
5.6.3. Simulation of Non-Random Consumer Selection
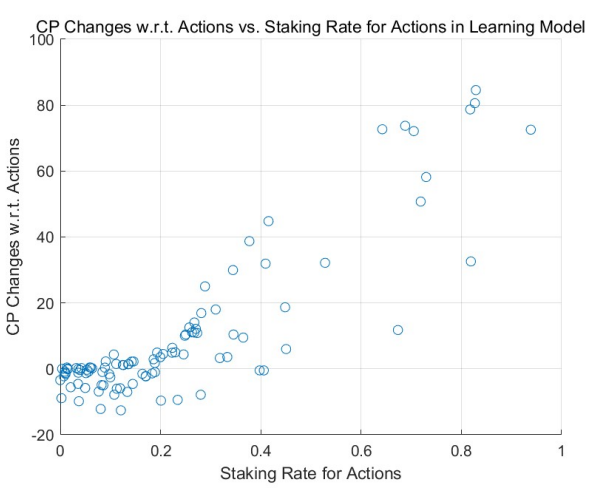
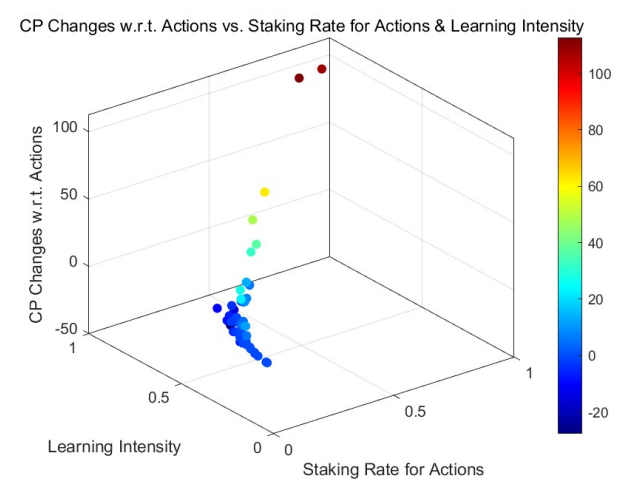
As elaborated in Section 4.2, the transparency of staking information naturally inclines consumers to favor producers who have staked a larger amount of credit points. Given that consumers inherently favor provider agents with a higher stake in credit points, it follows that those with minimal credit points staked for actions
are more likely to be overlooked and skipped by consumers, in line with the skipping mechanism delineated in Section 4.1 and Section 5.6.2. We now incorporate this skipping mechanism in simulating non-random consumer selection.
The MCSs elucidate the dynamics of credit points relative to the staking rate for actions, especially when consumer selection mechanisms are incorporated. Starting from a uniform initial distribution, the outcomes for the non-learning model are depicted in Figure 10, while the learning model outcomes are presented in Figure 11. Outcomes derived from the power-law initial distribution are similarly demonstrated in Figure 12 and Figure 13.
Across these simulations, a clear trend becomes evident: the influence of consumer selection mechanisms results in virtually negligible positive or negative returns for those who stake minimal credit points on actions. The patterns observed in the high staking rate regions, or the right half of the figures, align with previous observations: agents receiving positive returns are inclined to increase their stakes, whereas those incurring negative returns tend to reduce their staking rates, shifting towards the lower staking regions, i.e., the left sections of the figures.
This again tells, tasks tend to be more frequently allocated to individuals who stake a higher number of credit points for their actions. From a national economic standpoint, it is plausible to infer that these agents are more willing to commit to their actions, perhaps due to their specialized skills, or for other reasons. Consequently, they often receive positive ratings. On the flip side, those who are less specialized or consistently receive less favorable reviews find themselves marginalized over time. This evolving landscape resonates with the time-tested belief: ”the most specialized individuals handle the most specialized tasks.”
5.6.4. Contribution Incentive Mechanisms
MCSs with contribution incentive mechanisms indicate that the allocation of credit points for actions and ratings outside the system can dilute the credit points for others. However, the network effect, which brings competitive advantages among peers, can enhance the intrinsic value of each credit point. It is anticipated that if the incentive mechanism is designed appropriately, meaning the increase in credit points outweighs the dilution effect, then overall, everyone in the system stands to benefit.